Counterfactuals in the Probit Model

This post is about counterfactuals in the probit model. I wrote this while reading Pearl et al’s 2016 book Causal Inference in Statistics: A Primer.

The probit model with one normally distributed covariate can be written like this:

$\begin{array}{rcl} ϵ & \sim & N (0, 1) \\ X & \sim & N (0, 1) \\ Y ∣ X, ϵ & = & 1_{X + ϵ \geq 0} \end{array}$

Now we wish to find the density of the counterfactual $Y_{x}$ , see Pearl et al. (2016) for definitions. The density of $ϵ$ given $X = x$ and $Y = 1$ is

$\begin{array}{rcl} p (ϵ ∣ X = x, Y = 1) & = & \frac{p (x = x, Y = 1 ∣ ϵ) p (ϵ)}{p (x = x, Y = 1)} \\ = & \frac{p (Y = 1 ∣ ϵ, x = x) p (x = x) p (ϵ)}{p (x = x, Y = 1)} \\ \propto & 1_{x + ϵ \geq 0} p (x = x) p (ϵ) \end{array}$ or the normal density truncated to $[- x, \infty)$ , or $ϕ_{[- x, \infty)} (ϵ)$ .

Probability of Necessity

Now we’ll take a look at the probability of necessity. The most obvious way to generalize the probability of necessity to continuous distributions is to allow the counterfactual $x^{'}$ to be a parameter of the counterfactual $Y_{x^{'}}$ , like this:

$\begin{array}{rcl} P (Y_{x^{'}} = 0 ∣ X = x, Y = 1) & = & 1 - \int_{- x}^{\infty} 1_{x^{'} + ϵ \geq 0} ϕ_{[- x, \infty)} (ϵ) \\ = & 1 - \int_{max {- x, - x^{'}}}^{\infty} ϕ_{[- x, \infty)} (ϵ) d ϵ \\ = & 1 - \frac{min (Φ (x), Φ (x^{'}))}{Φ (x)} \end{array}$ Let’s plot this function.

x <- seq(-3, 3, by = 0.01)
x_hat <- 0

ps <- function(x, x_hat) 1 - pmin(pnorm(x_hat), pnorm(x))/pnorm(x_hat)

plot(x = x, y = ps(x, x_hat), 
     type = "l", 
     xlab = "Counterfactual x'",
     ylab = "Probability",
     main = "Counterfactual Probabilities, x = 0")
grid()
lines(x = x, y = ps(x, x_hat), type = "l")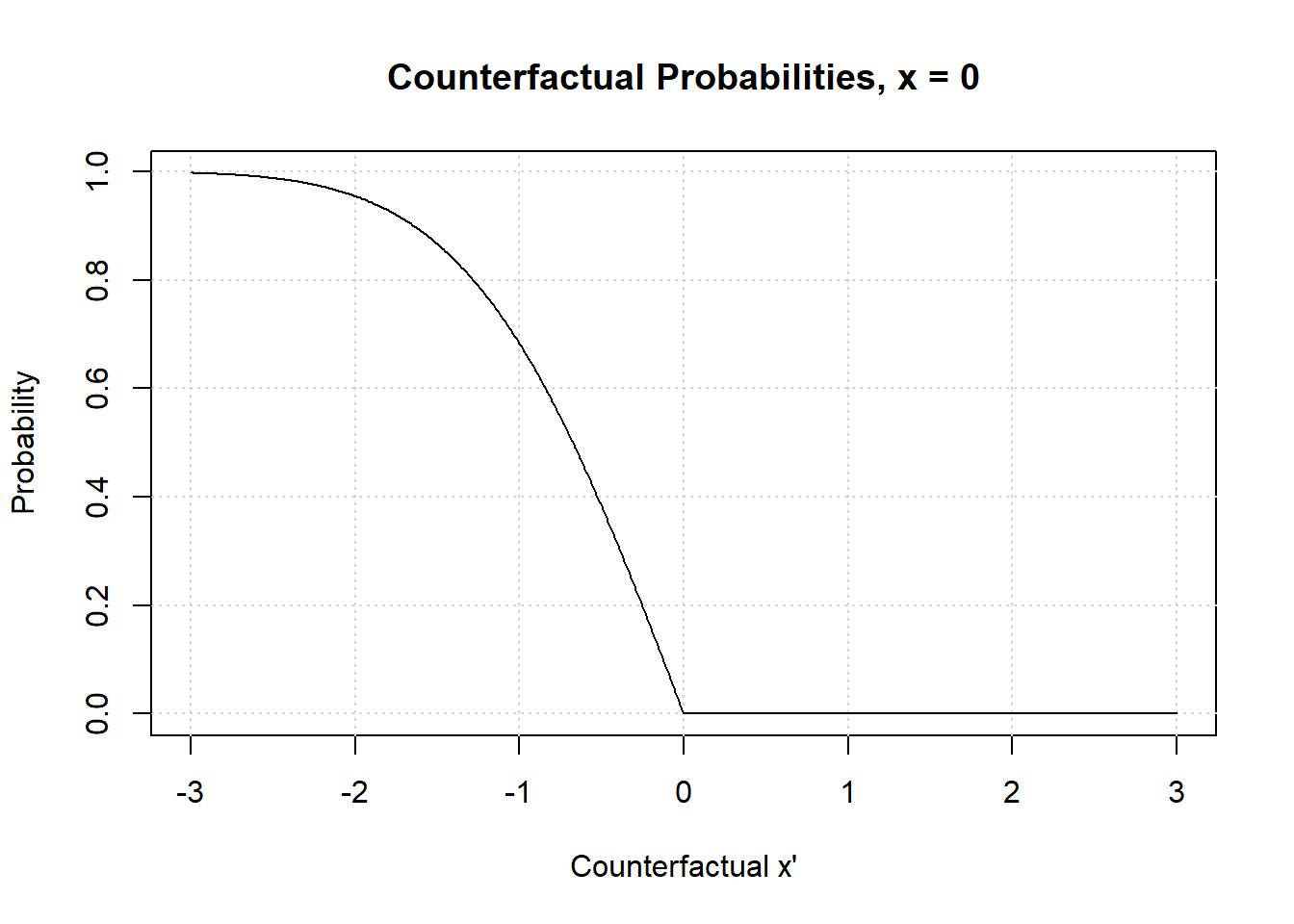

There is nothing too strange. The probability of necessity goes to $0$ as $x \to - \infty$ , which is what you would expect. For the probability of $Y = 1$ becomes really slim as $x \to - \infty$ . When $x^{'} > 0$ the probability of necessity is $0$ , as you will always observe $Y = 1$ counterfactually when $X = x^{'}$ if you observed $Y = 1$ with $X = x!$

Integrated Probability of Necessity

A more complicated question is: What rôle did the fact that $X = x$ have in $Y = 1$ ? Or, if $X$ wasn’t $x$ , what would $Y$ have been? With some abuse of notation, $P (Y_{X^{'}} = 0 ∣ X = x, Y = 1)$ answers this question, where $X^{'}$ is an independent copy of $X$ .

$\begin{array}{rcl} P (Y_{X^{'}} = 0 ∣ X = x, Y = 1) & = & 1 - \int_{- \infty}^{\infty} \int_{max {- x, - x^{'}}}^{\infty} ϕ_{[- x, \infty)} (ϵ) ϕ (x^{'}) d x \\ = & 1 - \int \frac{min (Φ (x), Φ (x^{'}))}{Φ (x)} ϕ (x^{'}) d x \\ = & 1 - \int_{x}^{\infty} ϕ (x^{'}) d x - \frac{1}{Φ (x)} \int_{- \infty}^{x} Φ (x^{'}) ϕ (x^{'}) d x \\ = & 1 - Φ (- x) - \frac{1}{2} \frac{1}{Φ (x)} [Φ (x) - Φ (x) Φ (- x)] \\ = & \frac{1}{2} Φ (x) \end{array}$

Now let’s plot this.

counter = function(x) 0.5*pnorm(x)

plot(x = x, 
     y = counter(x), 
     type = "l", 
     xlab = "Actual x",
     ylab = "Probability",
     main = "Counterfactual Probabilities")
grid()
lines(x = x, 
     y = counter(x), 
     type = "l")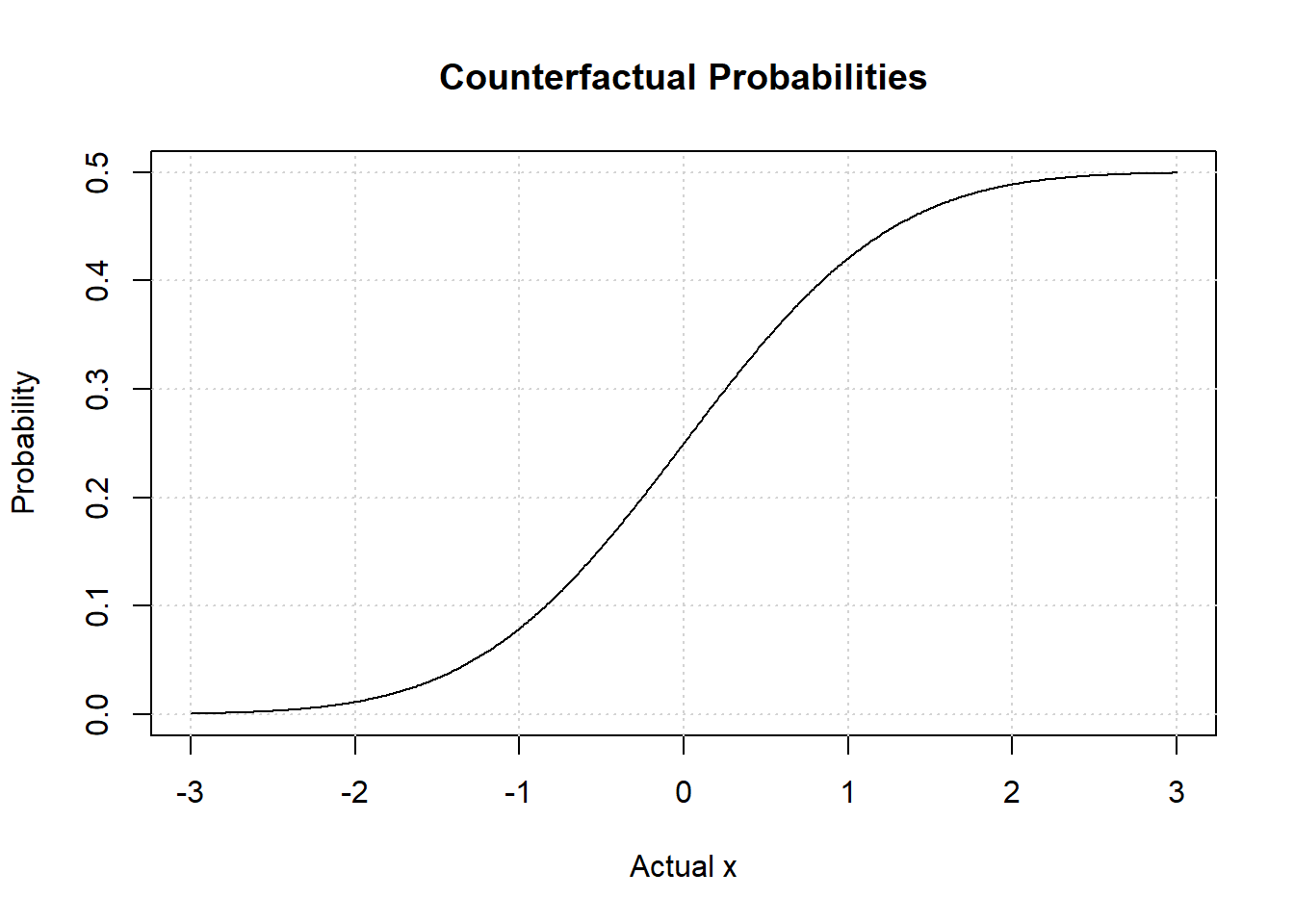

Notice the asymptote at $0.5$ . No matter how large $X = x$ we observe together with $Y = 1$ , we can never be more than $0.5$ certain that $Y = 0$ if we were to draw an $x$ once again. The asymptote at $0$ if we had observed at very small value $X = x$ together with $Y = 1$ , and we were to draw again, we would be really certain that $Y = 1$ would happen once again.